字符串入门
DFA
DFA,即确定有限状态自动机。用于判断输入的字符串是否符合要求。所有的字符串算法都是构造 DFA,结构有点像图灵机。
先给点定义:
- 状态集 $Q$(有限):若将自动机看成图,那么状态是顶点。
- 字符集 $\sum$:满足自动机要求的字符集。
- 可接受状态集 $F\subseteq Q$:是满足要求的状态。
- 初始状态 $q_0\in Q$:是初始空状态。
- 转移函数 $\delta$:$\delta\times \sum\rightarrow Q$ 是转移函数。
整个算法流程就是,从初始状态 $q_0$ 出发,每次输入字符 $c$,并通过转移函数 $\delta$ 转移。最后若状态为 $F$,那么字符串符合要求。
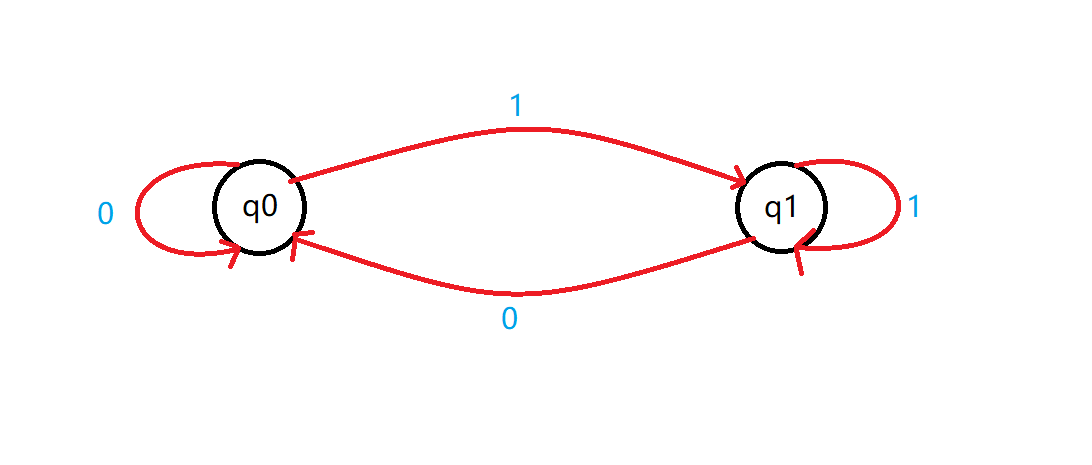
例题1:构造判断二进制数奇偶的 DFA
因为二进制数的奇偶性只与最后一位数是 $0$ 还是 $1$ 有关。所以这里构造的 DFA 用 $q$ 表示当前二进制数的奇偶性,每次输入的字符判断,如果是与当前 $q$ 相同就不变,否则转移到另一个。
字符串哈希
简单来说,就是通过一个函数(即 $\text{Hash}$)把字符串映射到整数,用来快速判断字符串相等。
其实我个人感觉 $\text{Hash}$ 虽然简单,但在不少题目中都挺有用的,比直接用 $\text{map}$ 少一个 $\log$。
具体实现的话,通常是使用多项式 $\text{Hash}$,也可以看成进制转换。设 $H(s)=\sum_{i=1}^ns_i\times base^{n-i}\ (mod\ M)$。
此时对于一个串 $\text{abcd},H(abcd)=a\times base^3+b\times base^2+c\times base+d$。
可以证明(我不会),模数为大质数的时候冲突概率最小。一般为保证正确率使用双模哈希,即两个模数得出的 $\text{Hash}$ 值都相等的情况下才相等。不过这样常数比较大,我喜欢用 $\text{unsigned long long}$ 自然溢出,代码要好写很多。
当询问子串 $\text{Hash}$ 时,重新计算的话就跟朴素暴力复杂度相同了,于是我们采取预处理的策略。我们使用类似前缀和的方式,设 $H_i=\sum_{j=1}^is_j^{i-j}$。这样要查询子串 $[l,r]$ 的 $\text{Hash}$ 值时,只需要用 $H_r-H_{l-1}\times base^{r-l+1}$。具体不赘述,读者自证不难。
例题1 最长回文子串
manacher 模板。
这个题的正解是 $\text{manacher}$ 线性解决,但是如果忘了怎么写,可以用二分+哈希水过。
复杂度是 $O(n\log n)$ 的,只需要加一个特判即可通过。特判是如果当前长度不匹配直接跳过,减少二分次数。
#include<bits/stdc++.h>
using namespace std;
#define ull unsigned long long
const int N=1.1e7+10;
const ull base=131;
char s[N];
ull h1[N],h2[N],p[N];
int n,ans;
ull hash1(int l,int r){
return h1[r]-h1[l-1]*p[r-l+1];
}
ull hash2(int l,int r){
return h2[l]-h2[r+1]*p[r-l+1];
}
int main(){
scanf("%s",s+1);
n=strlen(s+1);
p[0]=1;
for(int i=1;i<=n;++i){
p[i]=p[i-1]*base;
h1[i]=h1[i-1]*base+(ull)s[i];
}
for(int i=n;i>=1;--i){
h2[i]=h2[i+1]*base+(ull)s[i];
int r=min(n-i+1,i-1)+1,l=ans/2-1,mid;
if(l<=0||hash1(i-l,i-1)==hash2(i,i+l-1)){
while(l+1<r){
mid=(l+r)>>1;
if(hash1(i-mid,i-1)==hash2(i,i+mid-1)) l=mid;
else r=mid;
}
ans=max(ans,l*2);
}
r=min(n-i,i-1)+1,l=ans/2-1;
if(l<=0||hash1(i-l,i-1)==hash2(i+1,i+l)){
while(l+1<r){
mid=(l+r)>>1;
if(hash1(i-mid,i-1)==hash2(i+1,i+mid)) l=mid;
else r=mid;
}
ans=max(ans,l*2+1);
}
}
printf("%d\n",ans);
return 0;
}
|
字典树
字典树,就是像字典的树, 是一种用来处理字符串前缀的数据结构(当然也可以处理一些数据)。
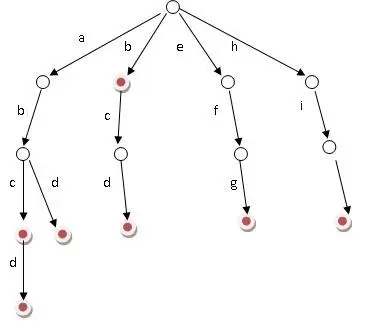
其结构是点为状态,边为转移。放到 DFA 上说,初始状态为 $q_0$,然后一个字符串中每读入一个字符就往后找并新建状态,转移就是这个字符。剩下的字符串,先找是否有状态可转移,没有再新建。
假设单词为:b,abc,abd,bcd,abcd,efg,hii
模板题的修改查询代码(有点像动态开点线段树)
int f(char x){
if(x>='A'&&x<='Z') return x-'A';
else if(x>='a'&&x<='z') return x-'a'+26;
else return x-'0'+52;
}
void insert(char s[]){
int p=0,len=strlen(s+1);
for(int i=1;i<=len;i++){
int c=f(s[i]);
if(!t[p][c]) t[p][c]=++tot;
p=t[p][c],cnt[p]++;
}
}
int find(char s[]){
int p=0,len=strlen(s+1);
for(int i=1;i<=len;++i){
int c=f(s[i]);
if(!t[p][c]) return 0;
p=t[p][c];
}
return cnt[p];
}
|
【题意】
给定一棵带边权树,求树上异或值最大的路径,路径的异或值定义为路径上边的异或和。输出最大值。
【解析】
先考虑路径异或和的转化,用 $w$ 表示,则 $w(u,v)=w(u,root)\oplus w(v,root)$。所以对于每一个点 $u$,要寻找与 $w(u,root)$ 异或值最大的 $w(v,root)$。那么我们先把所有 $w(u,root)$ 处理出来,然后根据二进制建字典树
一个二进制数要尽可能大,那就要让高位尽可能为 $1$,所以异或起来为 $1$ 代表两位不同,也就是说,从根开始向下搜索,尽可能找与 $w(u,root)$ 当前位不同的子树,这样保证最大。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
using namespace std;
#define F(i,x,y) for(int i=(x);i<=(y);++i)
#define Fo(i,x,y) for(int i=(x);i>=(y);--i)
const int N=1e5+10;
int n;
struct edge{
int v,next,w;
}e[N<<1];
int head[N],tot;
void add(int u,int v,int w){
e[++tot].v=v;
e[tot].w=w;
e[tot].next=head[u];
head[u]=tot;
}
int dis[N*32],cnt,ans;
int t[N*32][2];
void dfs(int u,int fa){
for(int i=head[u];i;i=e[i].next){
int v=e[i].v;
if(v==fa) continue;
dis[v]=dis[u]^e[i].w;
dfs(v,u);
}
}
void insert(int x){
int p=1;
Fo(i,30,0){
int c=(x>>i)&1;
if(!t[p][c]) t[p][c]=++cnt;
p=t[p][c];
}
}
int query(int x){
int p=1,tmp=0;
Fo(i,30,0){
int c=(x>>i)&1;
if(t[p][c^1]){
tmp=tmp*2+(c^1);
p=t[p][c^1];
}
else{
tmp=tmp*2+c;
p=t[p][c];
}
}
return tmp^x;
}
int main(){
cin>>n;
tot=ans=0;
cnt=1;
int x,y,z;
F(i,1,n-1){
cin>>x>>y>>z;
add(x,y,z);
add(y,x,z);
}
dfs(1,0);
F(i,1,n) insert(dis[i]);
F(i,1,n) ans=max(ans,query(dis[i]));
cout<<ans<<endl;
return 0;
}
|
KMP
KMP 是三位科学家共同设计的单模式串匹配算法。简单来说,就是用来快速查询字符串 $S$ 在 $T$ 中的出现次数、位置等信息。
我们定义一个字符串的前缀函数 $\pi$,$\pi_i$ 表示字符串 $S$(下标从 $0$ 开始)$s[0,i]$ 中最长的真前缀等于真后缀的长度。特别地,默认 $\pi_0=0$。
举个例子,对于 $S=abcabca$,其前缀函数为 $[0,0,0,1,2,3,4]$。详细过程可自行模拟。
朴素计算前缀函数时间复杂度是 $O(nm)$ 的,十分不优秀。考虑优化的话,我们发现没必要在失配以后从头匹配,可以直接在某个匹配了一部分字符的基础上再次尝试。根据这个想法,KMP 算法如下。
先预处理出前缀函数,再每次根据前缀函数匹配,失配则从当前位置的前缀函数位置开始往后匹配。时间复杂度 $O(n+m)$(但我并不会证明)。
正确性在于:每次找到前缀函数,前缀函数开始的一些字符与当前匹配好的一些字符是相等的,所以无错。
匹配部分(代码中的 $nex$ 数组就是前缀函数,$a$ 是文本串,$b$ 是模式串):
for(int i=1,j=0;i<=n;++i){
while(j&&b[j+1]!=a[i]) j=nex[j];
if(b[j+1]==a[i]) ++j;
if(j==m) ans[++cnt]=i-m+1;
}
|
预处理怎么做?自己跟自己匹配!
for(int i=2,j=0;i<=m;++i){
while(j&&b[j+1]!=b[i]) j=nex[j];
if(b[j+1]==b[i]) ++j;
nex[i]=j;
}
|
模板题完整代码:
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int N=1e6+10;
int n,m;
char a[N],b[N];
int nex[N],ans[N],cnt;
int main(){
scanf("%s%s",a+1,b+1);
n=strlen(a+1),m=strlen(b+1);
for(int i=2,j=0;i<=m;++i){
while(j&&b[j+1]!=b[i]) j=nex[j];
if(b[j+1]==b[i]) ++j;
nex[i]=j;
}
for(int i=1,j=0;i<=n;++i){
while(j&&b[j+1]!=a[i]) j=nex[j];
if(b[j+1]==a[i]) ++j;
if(j==m) ans[++cnt]=i-m+1;
}
for(int i=1;i<=cnt;++i) cout<<ans[i]<<endl;
for(int i=1;i<=m;++i) cout<<nex[i]<<" ";
return 0;
}
|
【解析】
先求出前缀函数,再考虑 DP。设 $f_i$ 表示到 $i$ 的答案,则 $f_i$ 的取值只有 $i$ 或者 $f_{\pi_i}$,因为至少要对 $\pi_i$ 覆盖才能覆盖 $i$。考虑什么时候为 $f_{\pi_i}$(此时答案肯定不劣),当且仅当有一个 $f_j=f_{\pi_i},i-j\le \pi_i$,表示既然要求覆盖 $i$,那么 $s[0,\pi_i]=s[i-\pi_i+1,i]$,也就是如果在 $[i-\pi_i+1,i]$ 内也可以用 $\pi_i$ 覆盖就可以覆盖 $i$。
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
const int N=5e5+10;
string s;
int n;
int fail[N],t[N],f[N];
signed main(){
cin>>s;
n=s.size();
s=" "+s;
for(int i=2,j=0;i<=n;++i){
while(j&&s[i]!=s[j+1]) j=fail[j];
if(s[i]==s[j+1]) ++j;
fail[i]=j;
}
f[1]=t[1]=1;
for(int i=2;i<=n;++i){
f[i]=i;
if(t[f[fail[i]]]>=i-fail[i]) f[i]=f[fail[i]];
t[f[i]]=i;
}
cout<<f[n]<<endl;
return 0;
}
|
后缀数组
设 $sa_i$ 表示按字典序排序后第 $i$ 小的后缀的编号,$rk_i$ 表示后缀 $i$ 的排名。
其中 $sa$ 数组也就是后缀数组,算法的本质就是快速求 $sa$ 数组。
两个数组满足:$sa[rk[i]]=rk[sa[i]]=i$。其实就是互为反数组(类似反函数)。
朴素做法
就是比较朴素,将 $n$ 个后缀直接 $\text{sort}$ 排序。排序复杂度是 $O(n\log n)$,再加上字符串排序比较字典序是 $O(n)$ 的,总复杂度 $O(n^2\log n)$。
优化1
直接排序复杂度不能接受,考虑倍增优化。
首先对字符串 $s$ 的所有长度为 $1$ 的子串排序得到初始的 $sa$ 和 $rk$。
接下来,枚举次幂(设当前倍增到 k),那么用上一次得到的 $rk_i$ 和 $rk_{i+k}$ 作为第一关键字与第二关键字(如果没有第二关键字直接补 $0$),$\text{sort}$ 排序得到新的 $sa$。
因为排序后 $rk_i$ 表示的是 $[i,i+k-1]$ 的信息,而 $rk_{i+k}$ 表示 $[i+k+1,i+2*k]$ 的信息,所以合并是正确的。
放个图方便理解。
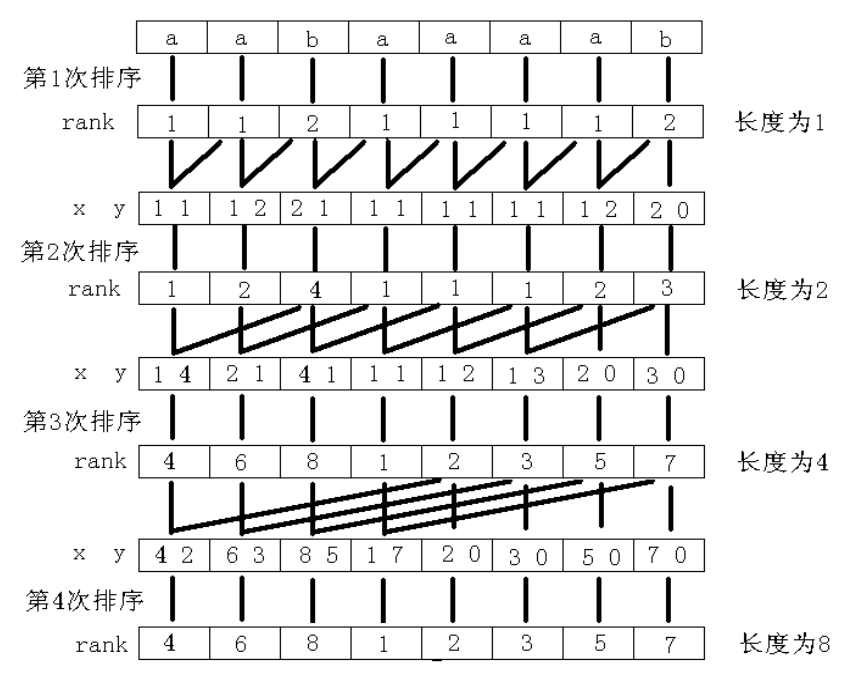
倍增的复杂度是 $O(\log n)$,每次 $\text{sort}$ 是 $O(n\log n)$,总时间复杂度 $O(n\log^2n)$。
优化2
$\text{sort}$ 是 $O(n\log n)$ 的,使用基数排序 $O(n)$,总复杂度 $O(n\log n)$。
贴个代码。
#include<bits/stdc++.h>
using namespace std;
#define F(i,x,y) for(int i=(x);i<=(y);++i)
#define Fo(i,x,y) for(int i=(x);i>=(y);--i)
const int N=1e6+10;
int n,m=122,cnt;
char s[N];
int x[N],y[N],sa[N],c[N];
bool cmp(int i,int j,int w){
return (y[i]==y[j])&&(y[i+w]==y[j+w]);
}
void SA(){
F(i,1,n) c[x[i]=s[i]]++;
F(i,2,m) c[i]+=c[i-1];
Fo(i,n,1) sa[c[x[i]]--]=i;
for(int k=1;;k<<=1,m=cnt){
cnt=0;
F(i,n-k+1,n) y[++cnt]=i;
F(i,1,n) if(sa[i]>k) y[++cnt]=sa[i]-k;
F(i,1,m) c[i]=0;
F(i,1,n) c[x[i]]++;
F(i,2,m) c[i]+=c[i-1];
Fo(i,n,1) sa[c[x[y[i]]]--]=y[i],y[i]=0;
F(i,1,n) y[i]=x[i];
cnt=1,x[sa[1]]=1;
F(i,2,n) x[sa[i]]=cmp(sa[i],sa[i-1],k)?cnt:(++cnt);
if(cnt==n) break;
}
}
int main(){
scanf("%s",s+1);
n=strlen(s+1);
SA();
F(i,1,n) printf("%d ",sa[i]);
return 0;
}
|



