网络流入门

写在前面

本文是笔者第一次学习网络流写的 $\text{blog}$，可能比较简陋，但还是尽可能让所有人看懂 qwq。

本篇主要介绍网络流算法，具体题目的建模可以看这一篇。

网络流引入

网络流，简单来说就是在一个很多水管的地方，水流从起点流向终点，在水管有多种限制的情况下最大化总流量。

网络

一个有向图 $G=(V,E)$，满足以下两个条件则为网络。

$1.$ $\forall e=(u,v)\in E$（称为弧），都有一个称为容量的值 $w=c(u,v)$，也可记作弧 $(u,v,w)$。
$2.$ 此图内有且仅有一个起点（源点）$S$ 和终点（汇点）$T$。

流

我们记 $f(u,v)$ 表示 $u$ 到 $v$ 的流量。
对于网络中的一个路径，满足以下两个条件则为流。

$1.$ 容量限制：对于路径上的每条边，流经该边的流量不能超过其容量，即 $f(u,v)\le c(u,v)$。感性理解为水管粗细有限，只能接受一定量的水流。
$2.$ 流量守恒：除了源点 $S$ 与汇点 $T$，路径上的每个点流入流量等于流出流量，即 $\sum_vf(u,v)=\sum_xf(x,u)$。感性理解为水管不能储存水，也不能凭空变出水。

残量网络

一个网络经过流的操作就变成残量网络。

我们用 $r(u,v)$ 表示残量网络，一开始 $r(u,v)=c(u,v)$。其实就是边的剩余容量。

对于每一次流的操作，$r(u,v)-=f(u,v)$。

因为流的相对性，一个流 $f(u,v)=x$，也同时会让反向边 $f(v,u)=-x$，这一点被称为反对称性。

所以对于一次流，$f(u,v)+=x$，$f(v,u)-=x$，$r(u,v)-=x$，$r(v,u)+=x$。

增广路

在残量网络中，找到一条从 $S$ 到 $T$ 的路径，其中所有边剩余容量都不为 $0$，则称此路径为增广路。

简单来说，就是没流满，还能流，使答案增加的路径。

而当一个残量网络中不存在增广路，则此时汇点得到的流量就是网络中的最大流。

反悔操作

上面好像是很完备的定义吧……等等，为什么 $r(v,u)+=x$，剩余容量还会增加？

原因是下一次再流的时候会抵消掉这一次的流量，相当于无事发生，也就是所谓反悔操作。

理解一下，反向边的设定和反悔操作其实是为了避免直接贪心导致的错误答案。

我们先看个图，红色边表示原边，绿色边表示反向边，边上的数字表示剩余容量。

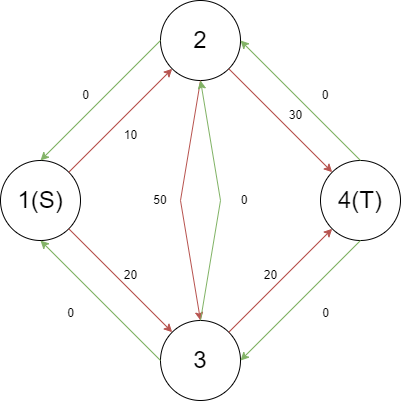
然后我们先尝试增广路径 $(1,2,3,4)$，流量为 $10$，则残量网络如下（注意反向边的剩余容量增加）。

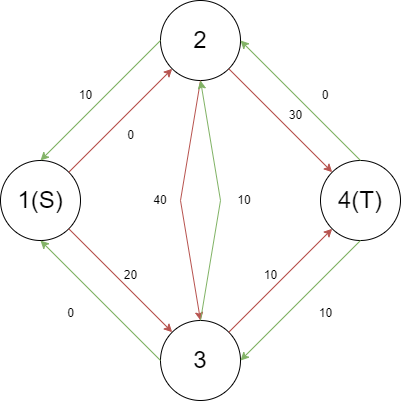
我们再增广路径 $(1,3,4)$，流量为 $10$。

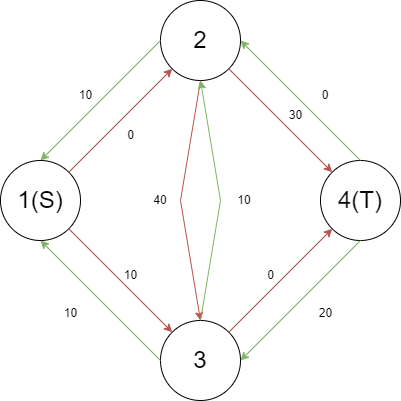
如果没有反向边，已经返回了错误答案 $20$。但现在我们发现，图竟然还能增广，路径 $(1,3,2,4)$，流量为 $10$。

唯一的区别是这一次路径上有一条反向边，流过此边表示反悔操作，得到最大流 $30$。

这样流和直接增广 $(1,2,4)$ 与 $(1,3,4)$ 答案相同，避免了顺序问题导致的答案错误。

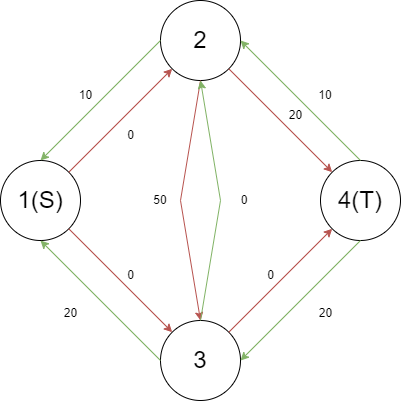
最大流

FF 算法

每次在残余网络中利用 $\text{dfs}$ 任意找一条从源点 $s$ 到汇点 $t$ 的增广路，直至不存增广路为止。

每次 $\text{dfs}$ 的复杂度是 $O(m)$ 的，可能有数据会卡到每次只能增广 $1$。如下图。

这个图中可能会因顺序导致一直在走 $(1,2,3,4)$ 和 $(1,3,2,4)$，每次只增广 $1$。

这样算法的复杂度是 $O(m\times \max w)$ 的。

#include <bits/stdc++.h>
using namespace std;
const int INF = 0x7fffffff;
const int N = 10000 + 10;
const int E = 100000 + 100;
struct Edge{
    int u, v, w, next;
};
Edge e[2 * E];
int Flow[N];
int h[N];
int vis[N];
int n, m, s, t, tot = -1;
int Maxflow = 0;
inline void Add(int u, int v, int w){
    e[++tot].u = u;
    e[tot].v = v;
    e[tot].w = w;
    e[tot].next = h[u];
    h[u] = tot;
}
int dfs(int u, int minf){
    if (u == t || minf == 0)
        return minf;
    vis[u] = 1;
    for (int i = h[u]; i != -1; i = e[i].next){
        int v = e[i].v;
        int w = e[i].w;
        if (w && !vis[v]){
            int f = dfs(v, min(minf, w));
            if (f > 0){
                e[i].w -= f;
                e[i ^ 1].w += f;
                return f;
            }
        }
    }
    return 0;
}
void FF(){
    Maxflow = 0;
    while (1){
        memset(vis, 0, sizeof(vis));
        int f = dfs(s, INF);
        if (f == 0)
            return;
        Maxflow += f;
    }
}
int main(){
    scanf("%d%d%d%d", &n, &m, &s, &t);
    memset(h, -1, sizeof(h));
    for (int i = 0; i < m; i++){
        int u, v, w;
        scanf("%d%d%d", &u, &v, &w);
        Add(u, v, w);
        Add(v, u, 0);
    }
    FF();
    printf("%d\n", Maxflow);
    return 0;
}

（此代码经格式化）

EK 算法

$\text{dfs}$ 太呆啦！我们在 $\text{FF}$ 算法的基础上使用 $\text{bfs}$ 找增广路，此时每次找的都是最短的增广路。

复杂度证明：

每次寻找增广路复杂度 $O(m)$。

我们接下来证明每条边最多成为 $O(n)$ 次路径流量上界（即是该残量网络中该路径上的容量最小值）

首先，对于 $(u,v)$ 是流量上界，有 $d_u=d_v+1$。

而增广后，$r(u,v)=0$，如果想要再次使用这条边，必须要走反向边反悔，即 $d’_u=d’_v+1$。

但因为这条路径是最短的，所以 $d’_v\ge d_v$，所以 $d’_u\ge d_v+1$，推出 $d’_u\ge d_u+2$。

因此，每次增广都会使 $S$ 到 $(u,v)$ 的最短距离至少增加 $2$。

因为最短距离上界是 $O(n)$，所以增广次数上界也是 $O(n)$。对于所有边，总增广次数上界 $O(nm)$。

所以我们得到，$\text{EK}$ 算法的复杂度上界是 $O(nm^2)$。

实际上这个上界很松，可以跑过 $10^3-10^4$。

我的证明并不严格，更加好的证明可以上 $\text{wiki}$ 查看 qwq。

给出模板题的代码实现。

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
#define F(i,x,y) for(int i=(x);i<=(y);++i)
#define Fo(i,x,y) for(int i=(x);i>=(y);--i)
const int N=2e5+10;
const ll INF=1e18;
struct edge{
    int v,next;
    ll w;
}e[N<<1];
int head[N],tot=1;
//这里 tot=1 是为后面反向边通过异或查找设置的
void add(int u,int v,ll w){
    e[++tot]={v,head[u],w};
    head[u]=tot;
}
int n,m,s,t;
int flag[205][205],pre[N],vis[N];
ll d[N];
bool bfs(){//找增广路
    F(i,1,n) vis[i]=0;
    queue<int> q;
    q.push(s);
    vis[s]=1,d[s]=INF;
    while(!q.empty()){
        int u=q.front();
        q.pop();
        for(int i=head[u];i;i=e[i].next){
            int v=e[i].v;
            ll w=e[i].w;
            if(w==0||vis[v]) continue;
            d[v]=min(d[u],w);//容量上界为路径剩余容量最小值
            pre[v]=i;//记录从哪条边来的
            q.push(v);
            vis[v]=1;
            if(v==t) return 1;
        }
    }
    return 0;
}
signed main(){
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cin>>n>>m>>s>>t;
    int x,y;
    ll z,ans=0;
    F(i,1,m){
        cin>>x>>y>>z;
        if(flag[x][y]==0){//去重边
            add(x,y,z);
            add(y,x,0);
            flag[x][y]=tot;
        }
        else e[flag[x][y]-1].w+=z;
    }
    while(bfs()!=0){//有增广路
        int x=t;
        while(x!=s){//一路跳回源点修改剩余容量
            int v=pre[x];
            e[v].w-=d[t];
            e[v^1].w+=d[t];
            x=e[v^1].v;
        }
        ans+=d[t];
    }
    cout<<ans<<endl;
    return 0;
}