浅谈平衡树

Splay

splay：伸展树，通过一系列的旋转维护平衡性。

注意，splay不一定是严格的平衡。故操作大部分均摊时间复杂度 $O(logn)$

分3种情况讨论旋转：

$1.$ Zig $or$ Zag

$2.$ Zig-Zig $or$ Zag-Zag （一字型，从左偏树到右偏树)

$3.$ Zig-Zag $or$ Zag-Zig （之字形转成一字型）

容易发现，旋转后树的中序遍历没有改变

splay的只因本操作

旋转

无需分开写左旋右旋

inline void rotate(int x)
{
    int y=t[x].fa;
    int z=t[y].fa;
    int k=(rs(y)==x);
    t[z].son[rs(z)==y]=x;
    t[x].fa=z;
    t[y].son[k]=t[x].son[k^1];
    t[t[x].son[k^1]].fa=y;
    t[x].son[k^1]=y;
    t[y].fa=x;
    pushup(y);
    pushup(x);
}

查找

与二叉搜索树的查找相同，从根节点开始，如果要查询的值大于该点的值，递归右儿子，否则递归左二子。

如果找到了当前要查找的数，将此节点旋转到根节点上。

插入

如果出现过，节点的数量+1。

否则新建节点，找到合适位置插入。

插完以后旋转到根节点。

inline void insert(int v)
{
    int u=root,p=0;
    while(u)
    {
        p=u;
        u=t[u].son[v>t[u].val];
    }
    u=++cnt;
    if(p)
    {
        t[p].son[v>t[p].val]=u;
    }
    t[u].init(v,p);
    splay(u,0);
}

删除

先找到此数的前驱，旋转到根节点。

再找后继，旋转到根节点的右儿子。

当前根节点的右儿子的左二子即为要删除的点。

提取区间

提取区间 $[x,y]$ ，将 $x-1$ 旋转到根，将 $y+1$ 旋转到根节点的右儿子。那么根节点的右儿子的左子树即为要提取的区间。

注意，当 $x=0$ 时无 $x-1$ 这个元素，当 $y=n$ 时无 $y+1$ 这个元素，解决方法是加入两个“哨兵”，插入在 $0$ 和 $n+1$ 的位置。
inline void qu(int &l,int &r)
{
    l=getk(l);
    r=getk(r+2);
    splay(l,0);
    splay(r,l);
}

区间翻转

区间翻转即为将区间内所有节点的左右子树进行交换。

首先提取区间（见上一个操作），随后交换根节点右儿子的左子树上每个节点的左右儿子。
inline void pushdown(int p)
{
    if(t[p].lazy)
    {
        swap(ls(p),rs(p));
        t[ls(p)].lazy^=1;
        t[rs(p)].lazy^=1;
        t[p].lazy=0;
    }
}

P3391 【模板】文艺平衡树

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;

namespace fastio
{
    #define te template<typename T>
    #define tem template<typename T,typename ...Args>
    te inline static void read(T &x){x=0;int f=1;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-') f=-1;ch=getchar();}while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}if(f==-1) x=-x;}
    tem inline static void read(T& x,Args& ...args){read(x);read(args...);}
    te inline static void write(char c,T x){T p=x;if(!p) putchar('0');if(p<0){putchar('-');p=-p;}int cnt[105],tot=0;while(p){cnt[++tot]=p%10;p/=10;}for(int i=tot;i>=1;i--){putchar(cnt[i]+'0');}putchar(c);}
    tem inline static void write(const char c,T x,Args ...args){write(c,x);write(c,args...);}
}using namespace fastio;

#define ls(x) t[x].son[0]
#define rs(x) t[x].son[1]
const int N=1e5+10;
int n,m;

struct node
{
    int son[2],fa,val;
    int siz,lazy;
    void init(int a,int b)
    {
        val=a;
        fa=b;
        siz=1;
    } 
}t[N];

int root,cnt;

inline void pushup(int p)
{    
    t[p].siz=t[ls(p)].siz+t[rs(p)].siz+1;
}

inline void pushdown(int p)
{
    if(t[p].lazy)
    {
        swap(ls(p),rs(p));
        t[ls(p)].lazy^=1;
        t[rs(p)].lazy^=1;
        t[p].lazy=0;
    }
}

inline void rotate(int x)
{
    int y=t[x].fa;
    int z=t[y].fa;
    int k=(rs(y)==x);
    t[z].son[rs(z)==y]=x;
    t[x].fa=z;
    t[y].son[k]=t[x].son[k^1];
    t[t[x].son[k^1]].fa=y;
    t[x].son[k^1]=y;
    t[y].fa=x;
    pushup(y);
    pushup(x);
}

void splay(int x,int k)
{
    while(t[x].fa!=k)
    {
        int y=t[x].fa;
        int z=t[y].fa;
        if(z!=k)
        {
            if((rs(y)==x)^(rs(z)==y)) {rotate(x);}
            else {rotate(y);}
        }    
        rotate(x);
    }
    if(!k) root=x;
}

inline void insert(int v)
{
    int u=root,p=0;
    while(u)
    {
        p=u;
        u=t[u].son[v>t[u].val];
    }
    u=++cnt;
    if(p)
    {
        t[p].son[v>t[p].val]=u;
    }
    t[u].init(v,p);
    splay(u,0);
}

int getk(int k)
{
    int u=root;
    while(1)
    {
        pushdown(u);
        if(t[ls(u)].siz>=k)
        {
            u=ls(u);
        }
        else if(t[ls(u)].siz+1==k) return u;
        else
        {
            k-=t[ls(u)].siz+1;
            u=rs(u);
        }
    }
    return -1;
}

inline void qu(int &l,int &r)
{
    l=getk(l);
    r=getk(r+2);
    splay(l,0);
    splay(r,l);
}

void print(int u)
{
    pushdown(u);
    if(ls(u))
    {
        print(ls(u));
    }
    if(t[u].val>=1&&t[u].val<=n)
    {
        write(' ',t[u].val);
    }
    if(rs(u))
    {
        print(rs(u));
    }
}

int main()
{
    read(n,m);
    int l,r;
    for(int i=0;i<=n+1;++i) {insert(i);}
    while(m--)
    {
        read(l,r);
        qu(l,r);
        t[ls(r)].lazy^=1;
    }
    print(root);
    return 0;
}

FHQ-Treap

前言

Treap 这个词是由 Tree 和 Heap 组合形成的，可以看出 Treap 是查找树和堆的结合，因此中文叫树堆。

和其他平衡树一样，Treap 的中序遍历值单调不减；而根据堆的性质，每个结点的权小于两个子结点的权。

Treap 分为有旋和无旋两种，而无旋 Treap又叫 FHQ-Treap，主要通过分裂（split）和合并（merge）实现维护操作。

操作

1. 分裂（split）
分裂操作是将一个树分成 $x,y$ 两个树。$x$ 中每一个结点的值都小于 $k$，而 $y$ 中每一个结点的值都大于等于 $k$。复杂度 $O(logn)$

举个例子：

（此图盗自出自某dalao blog）

代码：
void split(int p,int _val,int &x,int &y)
{
    if(!p) x=y=0;
    else if(t[p].val<=_val)
    {
        split(t[p].r,_val,t[p].r,y);
        pushup(p);
        x=p;
    }
    else
    {
        split(t[p].l,_val,x,t[p].l);
        pushup(p);
        y=p;
    }
}

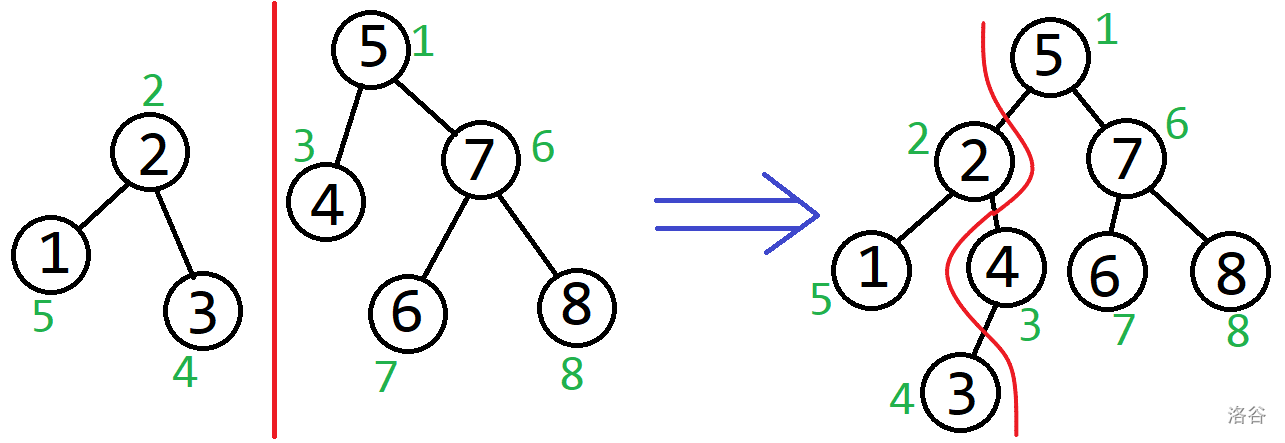
$2.$ 合并（merge）

合并是将 $x,y$ 两棵树合并为一棵树复杂度 $O(logn)$

merge

（此图盗自出自另一位dalao blog）

代码：

>int merge(int x,int y)
>{
   if(!x||!y) return x+y;
   if(t[x].key<=t[y].key)
   {
       t[x].r=merge(t[x].r,y);
       pushup(x);
       return x;
   }
   else
   {
       t[y].l=merge(x,t[y].l);
       pushup(y);
       return y;
   }
>}

$3.$ 插入
先将申请一个新的结点，作为一棵树 $y$；并将原来的树分裂成 $x,z$ 两棵树。
然后依次合并 $x,y,z$，就完成了。复杂度 $O(logn)$

代码：
inline void insert(int _val)
{
    int x,y;
    split(root,_val,x,y);
    t[++cnt].init(_val);
    root=merge(x,merge(cnt,y));
}

$4.$ 删除
删除比较巧妙，先将树分裂成 $x,y,z$ 三棵树；其中 $x$ 的每个结点的值均小于 $k$，$y$ 的每个结点的值均为 $k$，$z$ 的每个结点的值均大于 $k$ 。

直接合并 $y$ 的左右两棵子树，根节点就被删除掉了。最后，依次合并 $x,y,z$。

复杂度 $O(logn)$

代码：
inline void del(int _val)
{
    int x,y,z;
    split(root,_val,x,y);
    split(x,_val-1,x,z);
    z=merge(t[z].l,t[z].r);
    root=merge(x,merge(z,y));
}

$5.$ 查询排名
直接分裂，小于 $k$ 的树的大小加一即为排名。

复杂度 $O(logn)$
int getrank(int p,int _val)
{
    int x,y;
    split(root,_val-1,x,y);
    int res=t[x].siz+1;
    root=merge(x,y);
    return res; 
}

$6.$ 排名为 $x$ 的数
这个操作是查询第 $x$ 大,要按照普通的查询方法来搞

详见代码：
int getvalue(int p,int k)
{
    if(t[t[p].l].siz+1==k) return t[p].val;
    if(t[t[p].l].siz+1<k) return getvalue(t[p].r,k-t[t[p].l].siz-1);
    else return getvalue(t[p].l,k);
}

$7.$ 前驱

所以直接查找小于 $x$ 的数里最大的。

代码：

inline int prev(int _val)
{
    int x,y;
    split(root,_val-1,x,y);
    int tmp=x;
    while(t[tmp].r) tmp=t[tmp].r;
    root=merge(x,y);
    return t[tmp].val;
}

$8.$ 后继

于前驱同理，找大于等于 $x$ 里最小的

代码：

inline int nex(int _val)
{
    int x,y;
    split(root,_val,x,y);
    int tmp=y;
    while(t[tmp].l) tmp=t[tmp].l;
    root=merge(x,y);
    return t[tmp].val;
}

P3369 【模板】普通平衡树

#include<iostream>
#include<cstdio>
#include<ctime>
using namespace std;
namespace fastio
{
    #define te template<typename T>
    #define tem template<typename T,typename ...Args>
    te inline static void read(T &x){x=0;int f=1;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-') f=-1;ch=getchar();}while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}if(f==-1) x=-x;}
    tem inline static void read(T& x,Args& ...args){read(x);read(args...);}
    te inline static void write(char c,T x){T p=x;if(!p) putchar('0');if(p<0){putchar('-');p=-p;}int cnt[105],tot=0;while(p){cnt[++tot]=p%10;p/=10;}for(int i=tot;i>=1;i--){putchar(cnt[i]+'0');}putchar(c);}
    tem inline static void write(const char c,T x,Args ...args){write(c,x);write(c,args...);}
}using namespace fastio;
const int N=1e5+10;
int n,m;
int op,x;
int root,cnt;
struct node{
    int l,r,key,val,siz;    
    inline void init(int _val){
        val=_val;
        siz=1;
        key=rand();
    }
}t[N];
inline void pushup(int p){t[p].siz=t[t[p].l].siz+t[t[p].r].siz+1;}
void split(int p,int _val,int &x,int &y){
    if(!p) x=y=0;
    else if(t[p].val<=_val){
        split(t[p].r,_val,t[p].r,y);
        pushup(p);x=p;
    }else{
        split(t[p].l,_val,x,t[p].l);
        pushup(p);y=p;
    }
}
int merge(int x,int y){
    if(!x||!y) return x+y;
    if(t[x].key<=t[y].key){
        t[x].r=merge(t[x].r,y);
        pushup(x);return x;
    }else{
        t[y].l=merge(x,t[y].l);
        pushup(y);return y;
    }
}
inline void insert(int _val){
    int x,y;
    split(root,_val,x,y);
    t[++cnt].init(_val);
    root=merge(x,merge(cnt,y));
}
inline void del(int _val){
    int x,y,z;
    split(root,_val,x,y);
    split(x,_val-1,x,z);
    z=merge(t[z].l,t[z].r);
    root=merge(x,merge(z,y));
}
int getrank(int p,int _val){
    int x,y;
    split(root,_val-1,x,y);
    int res=t[x].siz+1;
    root=merge(x,y);return res; 
}
int getvalue(int p,int k){
    if(t[t[p].l].siz+1==k) return t[p].val;
    if(t[t[p].l].siz+1<k) return getvalue(t[p].r,k-t[t[p].l].siz-1);
    else return getvalue(t[p].l,k);
}
inline int prev(int _val){
    int x,y;
    split(root,_val-1,x,y);
    int tmp=x;
    while(t[tmp].r) tmp=t[tmp].r;
    root=merge(x,y);
    return t[tmp].val;
}
inline int nex(int _val){
    int x,y;
    split(root,_val,x,y);
    int tmp=y;
    while(t[tmp].l) tmp=t[tmp].l;
    root=merge(x,y);
    return t[tmp].val;
}
int main(){
    srand(time(0));
    read(n);
    while(n--){
        read(op,x); 
        if(op==1) insert(x);
        else if(op==2) del(x);
        else if(op==3) write('\n',getrank(root,x));
        else if(op==4) write('\n',getvalue(root,x));
        else if(op==5) write('\n',prev(x));
        else if(op==6) write('\n',nex(x));
    }
    return 0;
}

Splay

splay的只因本操作

旋转

查找

插入

删除

提取区间

区间翻转

P3391 【模板】文艺平衡树

FHQ-Treap

前言

操作

1​. 分裂（split）

$2.$ 合并 （merge）

$3.$ 插入

$4.$ 删除

$5.$ 查询排名

$6.$ 排名为 $x$ 的数

$7.$ 前驱

$8.$ 后继

P3369 【模板】普通平衡树

~~完结撒花~~

1. 分裂（split）

$2.$ 合并（merge）

完结撒花