并查集扩展
前言: 本文不再赘述朴素的并查集,主要记录一些并查集的题目做法和并查集算法扩展。
又称种类并查集。用于处理一些具有多个相互关系的并查集。一般朴素并查集判断是否在同一集合,扩域则判断多个集合的相互关系作用下(一般为排斥关系)是否在同一集合。本质上利用了并查集的传递性。
通俗地,朴素的并查集维护朋友,而扩域并查集可以维护朋友、敌人且满足敌人的敌人是朋友。
在并查集的边上定义某种权值、以及这种权值在路径压缩时产生的运算。一般来说,带权并查集时只能使用路径压缩优化,不过在比赛中一般不会卡这个。
题目描述
动物王国中有三类动物 $A,B,C$,这三类动物的食物链构成了有趣的环形。$A$ 吃 $B$,$B$ 吃 $C$,$C$ 吃 $A$。
现有 $N$ 个动物,以 $1 \sim N$ 编号。每个动物都是 $A,B,C$ 中的一种,但是我们并不知道它到底是哪一种。
有人用两种说法对这 $N$ 个动物所构成的食物链关系进行描述:
- 第一种说法是
1 X Y,表示 $X$ 和 $Y$ 是同类。
- 第二种说法是
2 X Y,表示 $X$ 吃 $Y$。
此人对 $N$ 个动物,用上述两种说法,一句接一句地说出 $K$ 句话,这 $K$ 句话有的是真的,有的是假的。当一句话满足下列三条之一时,这句话就是假话,否则就是真话。
- 当前的话与前面的某些真的话冲突,就是假话;
- 当前的话中 $X$ 或 $Y$ 比 $N$ 大,就是假话;
- 当前的话表示 $X$ 吃 $X$,就是假话。
你的任务是根据给定的 $N$ 和 $K$ 句话,输出假话的总数。
对于全部数据,$1\le N\le 5 \times 10^4$,$1\le K \le 10^5$。
题目解析
此题使用上述两种并查集皆可,下面分别讲解。
扩域并查集:
我们定义 $fa_x$ 表示集合,$y\in[1,n]$ 时表示 $x,y$ 是同类,$y\in[n+1,2n]$ 时表示 $y$ 吃 $x$,$y\in[2n+1,3n]$ 时表示 $x$ 吃 $y$。
这样我们发现,对于所有同类 $(x,y)$,其天敌 $(x+n,y+n)$ 在同一集合,同时其猎物 $(x+2n,y+2n)$ 也在同一集合。否则不满足条件,是假话。
这样就可以了,维护三种集合并判断,详见代码。
#include<bits/stdc++.h>
using namespace std;
const int N=5e4+10;
int f[3*N];
int n,k,ans;
int op,x,y;
int find(int x){
if(f[x]==x) return x;
return f[x]=find(f[x]);
}
void merge(int x,int y){
int xx=find(x),yy=find(y);
f[xx]=yy;
}
int main(){
scanf("%d%d",&n,&k);
for(int i=1;i<=3*n;++i) f[i]=i;
for(int i=1;i<=k;++i){
scanf("%d%d%d",&op,&x,&y);
if(x>n||y>n){
ans++;
continue;
}
if(op==1){
if(find(x+n)==find(y)||find(x+2*n)==find(y)) ans++;
else{
merge(x,y);
merge(x+n,y+n);
merge(x+2*n,y+2*n);
}
}
else{
if(find(x)==find(y)||find(x+2*n)==find(y)) ans++;
else{
merge(x,y+2*n);
merge(x+n,y);
merge(x+2*n,y+n);
}
}
}
printf("%d\n",ans);
return 0;
}
|
带权并查集:
用 $d_x$ 表示 $x$ 与 $fa_x$ 的关系,$0$ 表示同类,$1$ 表示捕食,$2$ 表示被捕食。
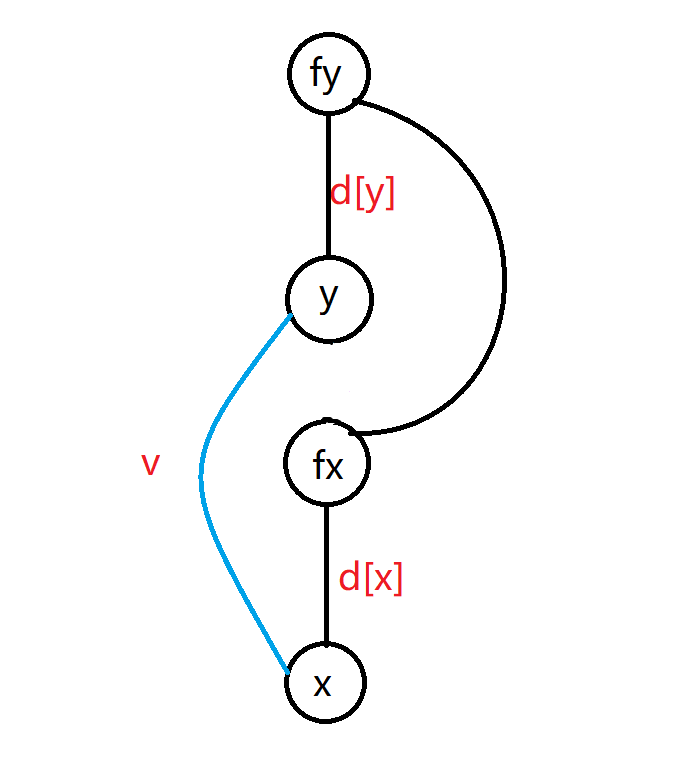
合并时,对于两点 $(x,y)$,权值关系为 $v$,设其父亲为 $(fx,fy)$。假设将 $fx$ 合并到 $fy$,则如图可知,$d_{fx}=d_y+v-d_x$。因为若将 $x$ 直接合并到 $y$,$d_x=d_y+v$,而现在是对于 $fx$ 合并到 $fy$,$x$ 的 $d$ 值应该相等,即 $d_x+d_{fx}=d_y+v$,移项后得上式。
#include<bits/stdc++.h>
using namespace std;
const int N=5e4+5;
int f[N],d[N],n,k,d1,x,y,ans;
int find(int x){
if(x!=f[x]){
int xx=f[x];
f[x]=find(f[x]);
d[x]=(d[x]+d[xx])%3;
}
return f[x];
}
int main(){
scanf("%d%d",&n,&k);
for(int i=1;i<=n;++i) f[i]=i,d[i]=0;
for(int i=1;i<=k;++i){
scanf("%d%d%d",&d1,&x,&y);
if((d1==2&&x==y)||(x>n||y>n)){
ans++;
continue;
}
if(d1==1){
if(find(x)==find(y)) if(d[x]!=d[y]) ans++;
else{
d[f[x]]=(d[y]-d[x]+3)%3;
f[f[x]]=f[y];
}
}
if(d1==2){
if(find(x)==find(y)) if(d[x]!=(d[y]+1)%3) ans++;
else{
d[f[x]]=(d[y]-d[x]+4)%3;
f[f[x]]=f[y];
}
}
}
printf("%d\n",ans);
}
|
题目描述
给定若干(至多 $26$ 个)小写字母表示的变量及其表示的二进制长度和两个 $01$ 串,串中字符保证只有 $0,1$ 和变量,求若两个字符串相等,有多少种变量取值。
题目解析
我们把两个串根据变量长度展开,然后根据确定的位置填数,并将对一个变量的固定修改下传到所有这个变量。使用并查集实现。
s:1bbaaaadddd1
t:aaaaccccbbee
变为(并查集维护)
s:1bb1aa1dddd1
t:1aa1cc1cbbe1
而剩下不确定的位置每个有两种可能,计算 $2$ 的次幂即可,注意需要高精度。
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
const int N=1e5+10;
int k,n,m,sum;
int len[30];
string a,b;
int x[N],y[N],fa[N];
#define ca(x) (int)(x-'a'+1)
int find(int x){
if(x==fa[x]) return x;
return fa[x]=find(fa[x]);
}
int p[N],top;
signed main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin>>k;
len[1]=2;
for(int i=2;i<=k+1;++i) cin>>len[i],sum+=len[i],len[i]+=len[i-1];
cin>>a>>b;
int tmp1,tmp2;
tmp1=a.size(),tmp2=b.size();
a=" "+a,b=" "+b;
for(int i=1;i<=tmp1;++i){
if(a[i]>='a'&&a[i]<='z'){
for(int j=len[ca(a[i])];j<len[ca(a[i])+1];++j) x[++n]=j;
}else x[++n]=a[i]-'0';
}
for(int i=1;i<=tmp2;++i){
if(b[i]>='a'&&b[i]<='z'){
for(int j=len[ca(b[i])];j<len[ca(b[i])+1];++j) y[++m]=j;
}else y[++m]=b[i]-'0';
}
if(n!=m) return cout<<0<<endl,0;
for(int i=1;i<=len[k+1];++i) fa[i]=i;
for(int i=1;i<=n;++i){
int fx=find(x[i]),fy=find(y[i]);
if(fx+fy==1){
cout<<0<<endl;
return 0;
}
if(fx!=fy){
fa[max(fx,fy)]=min(fx,fy);
sum--;
}
}
p[0]=1,top=1;
for(int i=1;i<=sum;++i){
for(int j=0;j<top;++j) p[j]<<=1;
for(int j=0;j<top;++j){
if(p[j]>=10){
p[j+1]+=p[j]/10;
p[j]%=10;
}
}
for(;p[top];++top){
p[top+1]+=p[top]/10;
p[top]%=10;
}
}
for(int i=top-1;i>=0;--i) cout<<p[i];
return 0;
}
|
题目描述
Alice 和 Bob 在玩一个游戏:他写一个由 $0$ 和 $1$ 组成的序列。Alice 选其中的一段(比如第 $3$ 位到第 $5$ 位),问他这段里面有奇数个 $1$ 还是偶数个 $1$。Bob 回答你的问题,然后 Alice 继续问。Alice 要检查 Bob 的答案,指出在 Bob 的第几个回答一定有问题。有问题的意思就是存在一个 $01$ 序列满足这个回答前的所有回答,而且不存在序列满足这个回答前的所有回答及这个回答。
对于 $100%$ 的数据,$1 \le n \leq 10^9$,$m \leq 5 \times 10^3$。
题目解析
这个数据范围也太小了,应该能用很多非正解方法过啊。
那么如果区间 $[i,j]$ 有奇数个 $1$,则 $[1,i-1]$ 和 $[1,j]$ 的奇偶性不同,反之同理。所以我们开始将区间左端点全部减一。问题变成查询左右端点奇偶性是否相同的问题。
使用扩域并查集,$[1,n]$ 表示与自己奇偶性相同的(朋友),$[n+1,2n]$ 表示与自己奇偶性不同的(敌人)。
于是对于朋友询问(even),若左端点是右端点敌人,或者右端点是左端点敌人,则有矛盾。敌人询问同理,合并操作即分别合并朋友和敌人的关系。
注意到数据范围,需要离散化。
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
const int N=1e5+10;
#define int ll
int n,m;
struct node{
int l,r,odd;
}a[N];
int b[N<<1],cnt;
int fa[N];
int find(int x){
if(x==fa[x]) return x;
return fa[x]=find(fa[x]);
}
void merge(int x,int y){
x=find(x),y=find(y);
if(x!=y) fa[x]=y;
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin>>n>>m;
char op[5];
for(int i=1;i<=m;++i){
cin>>a[i].l>>a[i].r>>op;
a[i].l--;
if(op[0]=='o') a[i].odd=1;
else a[i].odd=0;
b[++cnt]=a[i].l,b[++cnt]=a[i].r;
}
sort(b+1,b+1+cnt);
int len=unique(b+1,b+1+cnt)-(b+1);
for(int i=1;i<=len*2;++i) fa[i]=i;
int flag=0;
for(int i=1;i<=m;++i){
int x=lower_bound(b+1,b+1+len,a[i].l)-b;
int y=lower_bound(b+1,b+1+len,a[i].r)-b;
if(a[i].odd){
if(find(x)==find(y)||find(x+len)==find(y+len)){
cout<<i-1<<endl;
flag=1;
break;
}
merge(x+len,y),merge(x,y+len);
}
else{
if(find(x+len)==find(y)||find(y+len)==find(x)){
cout<<i-1<<endl;
flag=1;
break;
}
merge(x,y),merge(x+len,y+len);
}
}
if(!flag) cout<<m<<endl;
return 0;
}
|
题目描述
一个长度为 $n$ 的大数,用 $S_1S_2S_3 \cdots S_n$表示,其中 $S_i$ 表示数的第 $i$ 位, $S_1$ 是数的最高位。告诉你一些限制条件,每个条件表示为四个数,$l_1,r_1,l_2,r_2$,即两个长度相同的区间,表示子串 $S_{l_1}S_{l_1+1}S_{l_1+2} \cdots S_{r_1}$ 与 $S_{l_2}S_{l_2+1}S_{l_2+2} \cdots S_{r_2}$ 完全相同。
比如 $n=6$ 时,某限制条件 $l_1=1,r_1=3,l_2=4,r_2=6$ ,那么 $123123$,$351351$ 均满足条件,但是 $12012$,$131141$ 不满足条件,前者数的长度不为 $6$ ,后者第二位与第五位不同。问满足以上所有条件的数有多少个。对 $10^9+7$ 取模。
题目解析
我们对于每个条件,暴力循环,并将对应位置合并。
设最后的连通块个数是 $cnt$,则答案为 $9\times 10^{cnt-1}$,即第一位不能为 $0$,剩下的随便选。
复杂度 $O(nm\alpha)$,可以获得 $30pts$。
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
#define F(i,x,y) for(int i=(x);i<=(y);++i)
#define Fo(i,x,y) for(int i=(x);i>=(y);--i)
const int N=1e5+10,mod=1e9+7;
int n,m;
int l1[N],l2[N],r1[N],r2[N];
int fa[N];
int find(int x){
if(x==fa[x]) return x;
return fa[x]=find(fa[x]);
}
void merge(int x,int y){
x=find(x),y=find(y);
if(x!=y) fa[x]=y;
}
set<int> s;
signed main(){
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cin>>n>>m;
F(i,1,n) fa[i]=i;
F(i,1,m){
cin>>l1[i]>>r1[i]>>l2[i]>>r2[i];
F(j,l1[i],r1[i]) merge(j,l2[i]+j-l1[i]);
}
ll ans=1;
F(i,1,n){
if(s.count(find(i))==0){
if(i==1) ans=ans*9%mod;
else ans=ans*10%mod;
s.insert(find(i));
}
}
cout<<ans<<endl;
return 0;
}
|
发现时间复杂度瓶颈在于暴力合并,考虑优化。
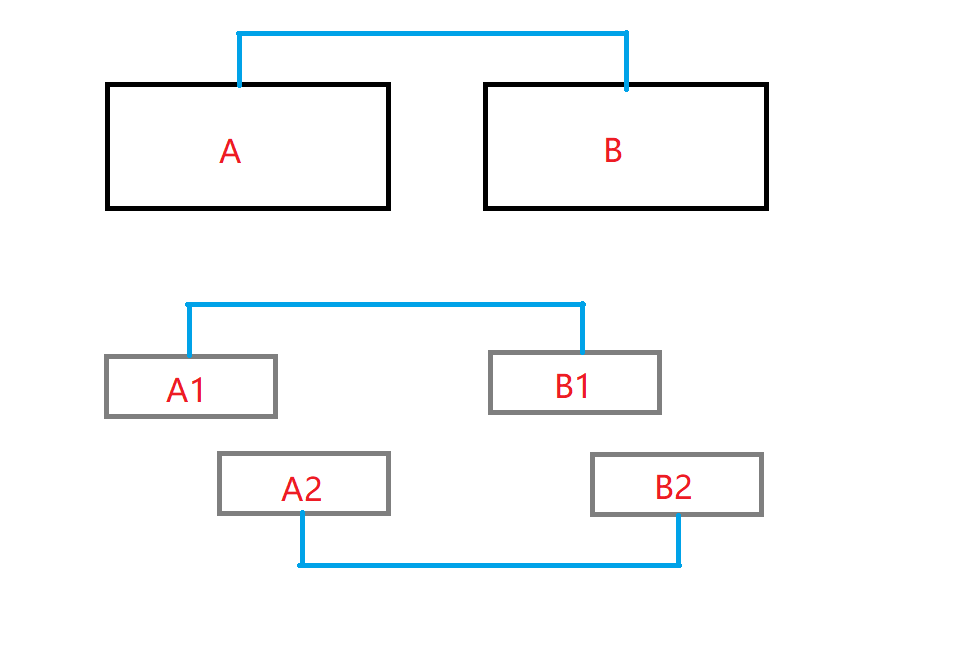
我们发现,合并两个并查集区间也可以转化为分别合并这两个区间的子区间(子区间之并等于原区间)。这被称为并查集合并的结合律(看图,上下两种合并等价)。
于是我们考虑用倍增维护这个关系,设 $f_{i,j}$ 表示从 $i$ 开始的 $2^j$ 个数的父亲。接下来可以看成把整个过程分成 $j$ 层,每一层向下递推合并关系,一直到 $0$ 层。
复杂度 $O(n\log n)$。
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
#define F(i,x,y) for(int i=(x);i<=(y);++i)
#define Fo(i,x,y) for(int i=(x);i>=(y);--i)
const int N=1e5+10,mod=1e9+7;
int n,m,l1,l2,r1,r2,cnt;
int fa[N][30],p[30],vis[N];
ll ans;
int find(int x,int k){
if(fa[x][k]==x) return x;
return fa[x][k]=find(fa[x][k],k);
}
void merge(int x,int y,int k){
x=find(x,k),y=find(y,k);
fa[x][k]=y;
}
ll ksm(ll a,ll b){
ll res=1;
while(b){
if(b&1) res=res*a%mod;
a=a*a%mod;
b>>=1;
}
return res;
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cin>>n>>m;
p[0]=1;
F(i,1,20) p[i]=p[i-1]<<1;
for(int j=0;p[j]<=n;++j)
for(int i=1;i+p[j]-1<=n;++i)
fa[i][j]=i;
F(i,1,m){
cin>>l1>>r1>>l2>>r2;
int j=log(r1-l1+1)/log(2);
merge(l1,l2,j);
merge(r1-p[j]+1,r2-p[j]+1,j);
}
Fo(j,log(n)/log(2),1){
for(int i=1;i+p[j]-1<=n;++i){
int f=find(i,j);
if(i==f) continue;
merge(i,f,j-1);
merge(i+p[j-1],f+p[j-1],j-1);
}
}
F(i,1,n){
int f=find(i,0);
if(!vis[f]){
cnt++;
vis[f]=1;
}
}
ans=ksm(10,cnt-1)*9%mod;
cout<<ans<<endl;
return 0;
}
|


