莫比乌斯反演
莫比乌斯反演
闲话
从听说莫反高高仰望,到现在总算理解了皮毛,不禁慨叹。所以,我要珍惜,不留遗憾。
尝试写一篇能让初学莫反的新人可以看懂的文章。
感受推柿子的魅力吧!
一些约定:
$\mu(x)$ 表示莫比乌斯函数。
$(x,y)$ 表示 $\gcd(x,y)$,即最大公约数。
$\left \lfloor a \right \rfloor$ 表示向下取整,即取小于 $a$ 的第一个整数。
$a|b$ 表示整除,$a$ 整除 $b$,也就是 $a$ 是 $b$ 的因数。
$[p]$ 表示若 $p$ 为真则为 $1$,否则为 $0$。
在推式子时,默认取 $n\le m$。
引入
莫反,就是通过反演形式更加方便地求函数的值。
原函数 $f$ 有一和函数 $F$,且 $F(n)=\displaystyle\sum_{d|n}f(d)$。我们的目标就是通过 $F$ 求 $f$。
先写几项
$$
\begin{aligned}
F(1)&=f(1)\\
F(2)&=f(1)+f(2)\\
F(3)&=f(1)+f(3)\\
F(4)&=f(1)+f(2)+f(4)
\end{aligned}
$$
我们类似解方程,用 $F$ 表示 $f$。
$$
\begin{aligned}
f(1)&=F(1)\\
f(2)&=F(2)-F(1)\\
f(3)&=F(3)-F(1)\\
f(4)&=F(4)-F(2)
\end{aligned}
$$
我们发现,$f(n)$ 可以表示为若干 $\pm F(\frac{n}{d})$ 的和(其中 $d|n$),所以我们将 $f(n)$ 表示为 $\displaystyle\sum_{d|n}\mu(d)F(\frac{n}{d})$。$\mu$ 函数是我们定义的系数函数,有 $-1,0,1$ 三种取值。
手推可得,$\mu(1)=1,\mu(2)=-1,\mu(3)=-1,\mu(4)=0$。
莫比乌斯反演
让我们寻找一些 $\mu$ 函数的性质。
我们发现,如果 $p\in prime$,$F(p)=f(p)+f(1)$,则 $f(p)=F(p)-f(1)=\mu(1)F(p)+\mu(p)F(1)$。可以得到 $\mu(p)=-1,\mu(1)=1$。
而当 $p\in prime$,$F(p^2)=f(1)+f(p)+f(p^2)$,得 $f(p^2)=F(p^2)-F(1)=\mu(1)F(p^2)+\mu(p^2)F(1)$。可以得到 $\mu(p^2)=0$。这个结论可以推广到 $\mu(p^k)=0$。
所以我们终于得到了 $\mu$ 函数的定义。
$$\mu(n)=\begin{cases}
1,\ n=1\\
(-1)^k,\ n\ 是\ k\ 个不同质因子的积(即没有平方因子) \\
0,\ n\ 有平方因子
\end{cases}$$
所以我们可以线性筛出 $\mu$ 函数的值。
vis[1]=1; |
下面讲解一些 $\mu$ 函数的性质,方便后面推式子。
- 性质 $1$
$\mu$ 函数是积性函数,即 $a,b$ 互质时 $\mu(ab)=\mu(a)\mu(b)$。
简单证明:
第一种情况:$a=1,\mu(a)=1$。
此时 $ab=b,\mu(ab)=\mu(b)=\mu(a)\mu(b)$ 成立。
第二种情况:$\mu(a)=0$。
此时 $ab$ 一定也至少有一个平方因子(来自 $a$),故 $\mu(ab)=0=\mu(a)\mu(b)$。
第三种情况:$\mu(a)=(-1)^n,\mu(b)=(-1)^m$。
因为 $a,b$ 互质,所以这两个数没有相同的质因子,也就是 $ab$ 中没有平方因子。故 $\mu(ab)=(-1)^{n+m}=\mu(a)\mu(b)$,成立。
- 性质 $2$
$F(n)=\displaystyle\sum_{d|n}\mu(d)=[n=1]$。
简单证明:
对于 $n=1$,显然成立。
对于 $n>1$,由性质 $1$,$\mu$ 是积性函数得其和函数 $F$ 也是积性函数。
设 $p\in prime,k\in N^*$。
可得 $F(p^k)=\displaystyle\sum_{d|p^k}\mu(d)=\mu(1)+\mu(p)+\mu(p^2)+…+\mu(p^k)=1+(-1)+0+…+0=0$。
分解 $n$,$n=p_1^{e_1}+p_2^{e_2}+…+p_k^{e_k}$,则 $F(n)=F(p_1^{e_1})F(p_2^{e_2})…F(p_k^{e_k})=0$。
- 性质 $3$
若 $f$ 是一个算数函数,$F$ 是其和函数,有 $F(n)=\displaystyle\sum_{d|n}f(d)$。
则有 $f(n)=\displaystyle\sum_{d|n}\mu(d)F(\frac nd)$。
此式称为莫比乌斯反演公式,也是莫反的灵魂所在。(感性理解看引入部分,严谨证明我不会 qwq。)
整除分块
在正式做题之前,先补点前置知识(会的大佬可以跳过这一部分)。
整除分块可以快速计算一些含有除法向下取整的和式,形如 $\displaystyle\sum_{i=1}^nf(i)g(\left \lfloor \frac{n}{i} \right \rfloor)$。
我们要做的,其实是利用整除的性质把结果相同的值打包计算。例如 $\left \lfloor \frac{3}{3} \right \rfloor=\left \lfloor \frac{4}{3} \right \rfloor=\left \lfloor \frac{5}{3} \right \rfloor=2$。
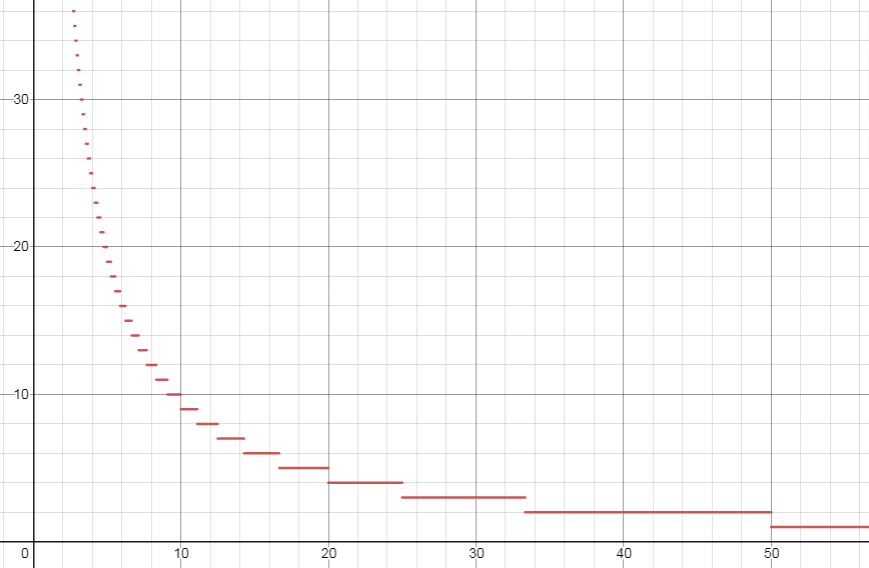
- 引理
对于常数 $n$,有 $i\le j\le n$。确定一个 $i$,使
$$\left \lfloor \frac{n}{i} \right \rfloor=\left \lfloor \frac{n}{j} \right \rfloor
$$
成立的最大 $j$ 为 $\left \lfloor \frac{n}{\left \lfloor \frac{n}{i} \right \rfloor} \right \rfloor$,即块右端点。
简单证明:
$\begin{cases}
设\ k=\left \lfloor \frac{n}{i} \right \rfloor\\
则\ i’=max\ i,且\ ik\le n
\end{cases}$
故 $i’=\left \lfloor \frac{n}{k} \right \rfloor=\left \lfloor \frac{n}{\left \lfloor \frac{n}{i} \right \rfloor} \right \rfloor$。
我们写出代码:
int ans=0; |
这样做时间复杂度是 $O(\sqrt n)$ 的。也就是说,最多有 $O(\sqrt n)$ 级别种 $\left \lfloor \frac{n}{i} \right \rfloor$ 的取值。
简单证明:
对于 $i\le \sqrt n$,显然只有 $\sqrt n$ 种取值。
对于 $i\ge \sqrt n$,$\left \lfloor \frac{n}{i} \right \rfloor\le \sqrt n$,所以也只有 $\sqrt n$ 种取值。
其实不止是向下取整,也有向上取证的整除分块,不过用途不如向下取整的广泛,感兴趣的读者可以自行了解。
题目选讲
注:有些题可以用别的方法做(比如欧拉函数,但本文只讨论莫反做法)。
例题 1 [SDOI2008] 仪仗队
形式化题意:
求 $\displaystyle \sum_{i=1}^{n}\sum_{j=1}^{n}[(i,j)=1]$
题目解析:
我们使用上文的性质3,将式子变化一下
$$\displaystyle \sum_{i=1}^{n}\sum_{j=1}^{n}[(i,j)=1]\\$$
由 $[(i,j)=1]\to\sum_{d|
(i,j)}\mu(d)$ 可得
$$\displaystyle \sum_{i=1}^{n}\sum_{j=1}^{n}\sum_{d|
(i,j)}\mu(d)$$
更换枚举顺序,先枚举 $d$,得
$$\sum_{d=1}\mu(d)\sum_{i=1}^n[d|i]\sum_{j=1}^n[d|j]$$
因为 $[1,n]$ 中 $d$ 的倍数有 $\left \lfloor \frac{n}{d} \right \rfloor$ 个,所以 $\sum_{i=1}^n[d|i]=\left \lfloor \frac{n}{d} \right \rfloor$
$$\sum_{d=1}\mu(d)\left \lfloor \frac{n}{d} \right \rfloor^2$$
把上界 $n,n$ 替换为 $n,m$ 同理,答案为
$$\sum_{d=1}\mu(d)\left \lfloor \frac{n}{d} \right \rfloor\left \lfloor \frac{m}{d} \right \rfloor$$
可以整除分块解决,时间复杂度 $O(n+T\sqrt n)$。
// [SDOI2008] 仪仗队 |
例题 2 GCD SUM
形式化题意:
求 $\displaystyle \sum_{i=1}^{n}\sum_{j=1}^{n}(i,j)$。
题目解析:
我们考虑枚举 $(i,j)$,记为 $d$。
$$\displaystyle \sum_{d=1}^nd\sum_{i=1}^{n}\sum_{j=1}^{n}[(i,j)=d]$$
让 $i,j$ 都除以 $d$,变为
$$\displaystyle \sum_{d=1}^nd\sum_{i=1}^{\left \lfloor \frac{n}{d} \right \rfloor}\sum_{j=1}^{\left \lfloor \frac{n}{d} \right \rfloor}[(i,j)=1]$$
后面的部分变成了例题 $1$
$$\displaystyle \sum_{d=1}^nd\sum_{g=1}^n\mu(g)\left \lfloor \frac{n}{dg} \right \rfloor^2$$
此时已经可以直接整除分块了,我们做进一步优化,设 $T=dg$
$$\displaystyle \sum_{d=1}^nd\sum_{g=1}^n\mu(g)\left \lfloor \frac{n}{T} \right \rfloor^2$$
先枚举 $T$,得
$$\displaystyle \sum_{T=1}^n\left \lfloor \frac{n}{T} \right \rfloor^2\sum_{d|T}d\mu(\frac{T}{d})$$
发现后面是欧拉函数(我收回不讲欧拉函数这句话)
$$\displaystyle \sum_{T=1}^n\phi(T)\left \lfloor \frac{n}{T} \right \rfloor^2$$
杜教筛可以进一步优化,但此题没必要了,复杂度线性。
// P2398 GCD SUM |
