Tarjan
以前只是背过了板子,很容易忘,所以认真学习一下。
本文记录 $\text{Tarjan}$ 算法在图论中的应用,以备忘和总结。
因为不可抗因素(本人太菜),文章有问题欢迎指出。
“把原理搞明白,不要死记硬背” ——金牌教练找事
强连通分量
- 强连通,指有向图 $G$ 中任意两个点之间都有路径可达。
- 强连通分量,指有向图中的极大强连通子图。
前置知识-$\text{dfs}$ 树
知周所众,有向图的 $\text{dfs}$ 树中边一般分为 $4$ 种。
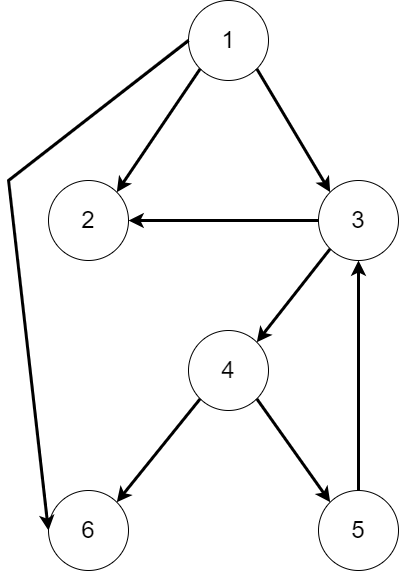
随机构造一个有向图(下文中的“父子”关系来源于 $\text{dfs}$ 树)。
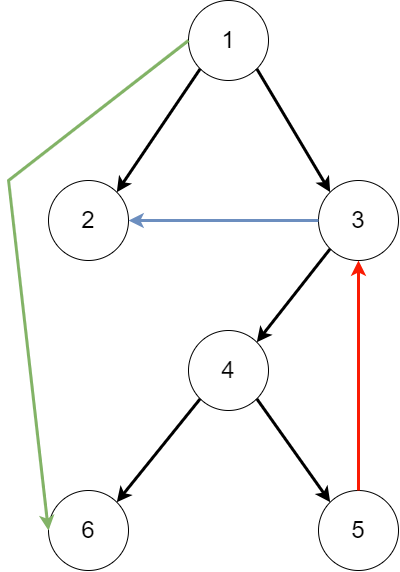
图中,黑边为树边,构成 $\text{dfs}$ 树;红边为反祖边,指子孙指向祖先的边;绿边为前向边,指祖先指向子孙的边;蓝边为横叉边,指走到一个访问过的结点,这个结点不是当前结点的祖先,两点之间的边(也就是旁系亲属)。
我们发现,若点 $u$ 是某个强连通分量中 $\text{dfs}$ 时走到的第一个点,那此点一定是这个强连通分量构成子树的根。(若不是,子树中一定有横叉边或者反祖边指向根,与假设“走到的第一个点”矛盾。)
Tarjan 求强连通分量
我们设出两个数组,$dfn_x$ 与 $low_x$,前者表示搜索时 $x$ 的 $\text{dfs}$ 序,后者表示以 $x$ 为根的子树中的结点通过一条非树边能到达点的 $dfn$ 的最小值。也就是 $min_{\normalsize y\in Subtree_x}dfn_k$,其中 $y\to k\in G$ 且 $\notin Dfs_tree$。
我们得到一个没什么用的性质:$\text{dfs}$ 树中向下的一条路径,$dfn$ 递增,$low$ 不减。
一个有用的性质:如果 $dfn_u=low_u$,则以 $u$ 为根的子树构成一个强连通分量,因为这说明 $u$ 点的 $dfn$ 最小,子树中的点没法跳出去。
为了维护强连通分量,我们采用栈,搜索到的节点入栈,闭环时弹出。
搜索过程中,对于 $u\to v$,分类讨论。
$1°$ $v\in son_u$,判断条件为没有访问过,即 $dfn_v=0$。向下搜索,并用 $low_v$ 更新 $low_u$,因为 $v$ 能到的 $u$ 也可以。
$2°$ $v\notin son_u$,这里要判断一下 $v$ 是否在栈中,不在说明 $v$ 所在的强连通分量已经处理过了,不用管。在栈中,用 $dfn_v$ 更新 $low_u$,表示 $u$ 可达子树外的点。
放个代码。$vis$ 表示是否在栈中,$ans$ 记录分量,$cnt$ 表示分量数,$scc$ 标记点在哪个分量里。
vector<int> e[N],ans[N];
int dfn[N],low[N],scc[N],vis[N],s[N],cnt,tot,top;
void tarjan(int u){
vis[u]=1;
dfn[u]=low[u]=++tot;
s[++top]=u;
for(int v:e[u]){
if(!dfn[v]){
tarjan(v);
low[u]=min(low[u],low[v]);
}
else if(vis[v]) low[u]=min(low[u],dfn[v]);
}
if(low[u]==dfn[u]){
cnt++;
while(s[top+1]!=u){
int t=s[top--];
vis[t]=0;
scc[t]=cnt;
ans[cnt].push_back(t);
}
}
}
|
割点与割边
- 割点:对于一个无向图,如果把一个点删除后图的极大连通分量数增加了,那么这个点称为割点。
- 割边:对于一个无向图,如果把一条边删除后图的极大连通分量数增加了,那么这条边称为割边。
Tarjan 求割点
先说结论:存在 $v\in son_u$ 使得 $dfn_u\le low_v$,则 $u$ 是割点。
原因很简单,对于这个儿子,无论怎样也跳不出这棵子树,那么把根删掉后至少多出现一个块。
但是对根节点不满足,因为一定跳不出根节点,所以特判,当且仅当根节点儿子数大于 $1$ 时,是割点(这一点不难想到)。
int dfn[N],low[N],flag[N],tot,ans;
vector<int> e[N];
void tarjan(int u,int fa){
int cnt=0;
dfn[u]=low[u]=++tot;
for(int v:e[u]){
if(!dfn[v]){
cnt++;
tarjan(v,u);
low[u]=min(low[u],low[v]);
if(low[v]>=dfn[u]&&!flag[u]&&u!=fa){
flag[u]=1;
ans++;
}
}
else low[u]=min(low[u],dfn[v]);
}
if(u==fa&&cnt>=2&&!flag[u]){
flag[u]=1;
ans++;
}
}
|
Tarjan 求割边
求割边的过程跟割点差不多,只需要把 $low_v\ge dfn_u$ 改成 $low_v> dfn_u$,也不用考虑根节点。
原理跟割点几乎一样,都是判断跳不出子树,不多赘述。
void tarjan(int u, int fa) {
father[u] = fa;
low[u] = dfn[u] = ++dfs_clock;
for (int i = 0; i < G[u].size(); i++) {
int v = G[u][i];
if (!dfn[v]) {
tarjan(v, u);
low[u] = min(low[u], low[v]);
if (low[v] > dfn[u]) {
isbridge[v] = true;
++cnt_bridge;
}
}
else if (dfn[v] < dfn[u] && v != fa) {
low[u] = min(low[u], dfn[v]);
}
}
}
|
双连通分量
点双联通:对于图中两点 $u,v$,如果删去图中除了这两个点之外的任意一点,都不能使这两个点不连通,那么称这两个点点双联通,极大的点双联通子图称为点双联通分量,其实就是没有割点。
边双联通:对于图中两点 $u,v$,如果删去图中除了这两个点之外的任意一边,都不能使这两个点不连通,那么称这两个点边双联通,极大的边双联通子图称为边双联通分量,即无桥极大子图。
注意,边双联通有传递性,但点双联通没有(点双反例如下)。
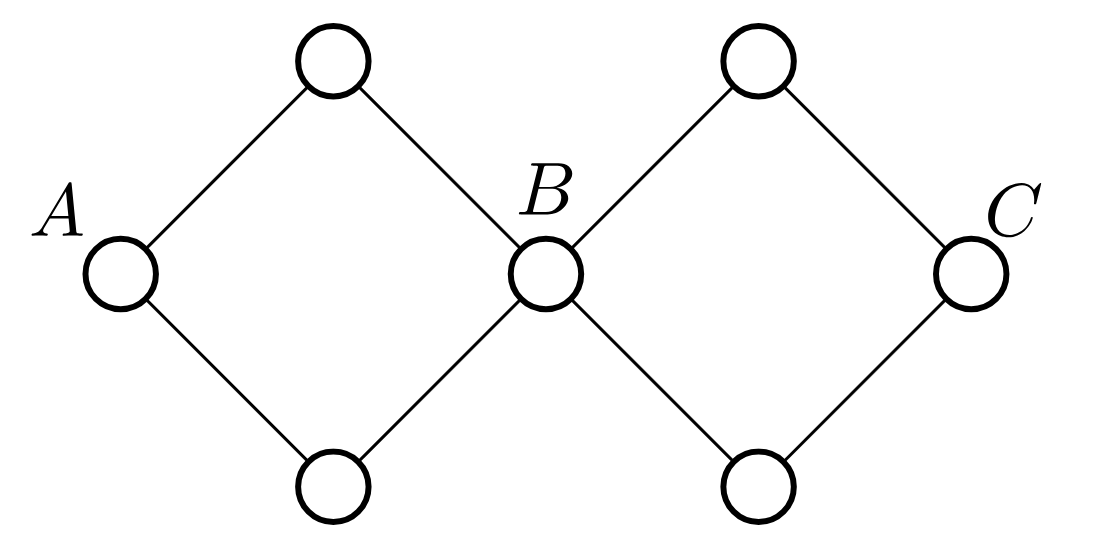
这里 $A,B$ 点双联通,$B,C$ 点双联通,但 $A,C$ 不点双联通。
边双
求法上,可以把桥删掉以后 $\text{dfs}$ 分离,也可以把边双当环找,代码是后者做法。时间复杂度 $O(n+m)$。
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
#define fi first
#define se second
const int N=5e5+10;
int n,m;
int dfn[N],low[N],s[N],tot,cnt,top;
vector<pair<int,int> > e[N];
vector<vector<int> > ans;
void tarjan(int u,int fa){
dfn[u]=low[u]=++tot;
s[++top]=u;
for(auto v:e[u]){
if(v.se==(fa^1)) continue;
if(!dfn[v.fi]){
tarjan(v.fi,v.se);
low[u]=min(low[u],low[v.fi]);
}
else low[u]=min(low[u],dfn[v.fi]);
}
if(dfn[u]==low[u]){
cnt++;
vector<int> tmp;
while(s[top+1]!=u)
tmp.push_back(s[top--]);
ans.push_back(tmp);
}
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin>>n>>m;
for(int i=1,x,y;i<=m;++i){
cin>>x>>y;
e[x].push_back(make_pair(y,i<<1));
e[y].push_back(make_pair(x,i<<1|1));
}
for(int i=1;i<=n;++i) if(!dfn[i]) tarjan(i,0);
cout<<cnt<<endl;
for(auto i:ans){
cout<<i.size()<<" ";
for(auto j:i) cout<<j<<" ";
cout<<endl;
}
return 0;
}
|
点双
先给出点双的两条性质:
讨论一下根和割点,割点则任意放到点双中(可能作为公共点);根有多种情况,单点不必多说,仅有一个子树则是点双的根,超过一个儿子就是割点。
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define endl '\n'
const int N=5e5+10;
int n,m;
int dfn[N],low[N],s[N],tot,cnt,top;
vector<int> e[N];
vector<vector<int> > ans;
void tarjan(int u,int fa){
int sum=0;
dfn[u]=low[u]=++tot;
s[++top]=u;
for(int v:e[u]){
if(!dfn[v]){
sum++;
tarjan(v,u);
low[u]=min(low[u],low[v]);
if(low[v]>=dfn[u]){
cnt++;
vector<int> tmp;
while(s[top+1]!=v) tmp.push_back(s[top--]);
tmp.push_back(u);
ans.push_back(tmp);
}
}
else low[u]=min(low[u],dfn[v]);
}
if(fa==0&&sum==0){
cnt++;
vector<int> tmp;
tmp.push_back(u);
ans.push_back(tmp);
}
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin>>n>>m;
for(int i=1,x,y;i<=m;++i){
cin>>x>>y;
e[x].push_back(y);
e[y].push_back(x);
}
for(int i=1;i<=n;++i) if(!dfn[i]) tarjan(i,0);
cout<<cnt<<endl;
for(auto i:ans){
cout<<i.size()<<" ";
for(auto j:i) cout<<j<<" ";
cout<<endl;
}
return 0;
}
|



